CONTOH PERTIDAKSAMAAN LINEAR

Oleh Diposting pada

KONSEP

Pertidaksamaan Linear, adalah suatu kalimat terbuka dalam matematika yang terdiri dari variabel berderajat satu dan dihubungkan dengan tanda pertidaksamaan.

BENTUK UMUM

  • ax + by > c
  • ax + by < c
  • ax + by ≥ c
  • ax + by ≤ c

Dengan a koefisien untuk x, b koefisien dari y dan c konstanta dimana a,b,c anggota bilangan riil dan a≠0,b≠0 .

METODE PENYELESAIAN

  • Biasanya penyelesaiannya digambarkan dengan grafik. Adapun langkah-langkahnya sebagai berikut :
  1. Ubah tanda ketidaksamaan menjadi persamaan
  2. Tentukan titik potong koordinat kartesius dengan sumbu x dan sumbu y.
  3. Gunakan titik uji untuk menentukan daerah penyelesaian.
  4. Gambarkan grafiknya dan beri arsiran pada daerah penyelesaiannya.

CONTOH SOAL DAN PENYELESAIAN

Gambarlah pada bidang cartesius, himpunan penyelesaian dari pertidaksamaan x + 2y ≤ 6 untuk x dan y ϵ R.

Jawab : Pertama kita gambar garis x + 2y =6. Untuk x = 0 maka akan diperoleh y = 3 sehingga diperoleh titik (0,3). Untuk y = 0 maka nilai x = 6 sehingga diperoleh titik (6,0). Lukis pada bidang kartesius dengan menghubungkan titik (0,3) dan (6,0).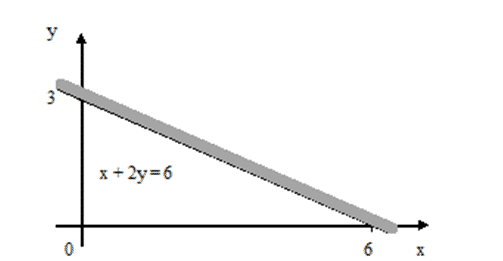 CONTOH SOAL PERTIDAKSAMAAN LINEAR

Garis tersebut membagi bidang cartesius menjadi dua bagian, masing masing merupakan daerah penyelesaian  x + 2y < 6 dan x + 2y > 6. Untuk menentukan belahan bidang yang merupakan penyelesaian dari soal diatas, ambil sembarang titik untuk di uji. Misalnya kita ambil titik (0,0)sebagai titik uji sehingga akan menjadi :

0 + 2. (0) < 6

0 + 0 < 6

0 < 6 (benar)

Karena pernyataan itu benar maka titik (0,0) adalah sebuah daerah penyelesaian x + 2y < 6. Dengan demikian himpunan penyelesaian dari pertidaksamaan x + 2y ≤ 6 adalah himpunan titik pada garis x + 2y =6 dan pada belahan yang memuat titik (0,0) sehingga himpunan penyelesaiannya diberikan pada gambar diatasyang merupakan daerah yang bersih (tidak diarsir).

Soal Terapan :

  1. Tina mempunyai 700 kartu dan Budi mempunyai 500 kartu. Masing-masing memberikan kartu kepada Lisa dalam jumlah yang sama. Sisa kartu yang dimiliki Tina lebih kecil atau sama dengan 3 kali sisa kartu yang dimiliki Budi. Tentukanlah jumlah masing-masing kartu yang diberikan kepada Lisa!

Jawab : misal : Tina dan Budi memberikan masing-masing x kartu, maka

Sisa kartu Tina = 700 – x

Sisa kartu Budi = 500 – x

Maka, 700 – x £ 3(500 – x)

700 – x £ 1500 – 3x

2x £ 800

x £ 400

Jadi, jumlah kartu yang diberikan kepada Lisa kurang dari sama dengan 400.

  1. KESIMPULAN
  • Kesimpulannya adalah, pertidaksaamaan linear memiliki bentuk umum ax + by > c; ax + by < c; ax + by ≥ c; dan ax + by ≤ c.
  • Pertidaksamaan Linear dapat diseleseaikan dengan menggunakan grafik
  • Pertidaksamaan linear dapat diterapkan dalam kehidupan seharai-hari.

Persamaan Linear

Persamaan linear disebut juga dengan persamaan garis lurus, karena grafik dari himpunan penyelesaiannya merupakan garis lurus.

Contoh 1:

x dan y disebut sebagai variabel  dimana x dan y berpangkat 1.

Contoh di atas merupakan kalimat terbuka belum dapat ditentukan benar atau salah nya jika variabel x dan y belum diganti dengan lambang bilangan real (nyata).

Persamaan Linear dengan Dua Variabel

Persamaan linear dengan dua variabel merupakan salah satu dari jenis persamaan linear yang memiliki dua buah variabel, atau suatu persamaan yang penyelesaiannya terdiri dari dua pengganti yang memenuhi kalimat itu menjadi benar dan grafik penyelesaiannya membentuk garis lurus.

Variabel atau peubah adalah lambang yang dapat diganti. Dalam menentukan pengganti, penyelesaian atuapun himpunan penyelesaian suatu persamaan senantiasa tidak bisa lepas dari pembahasan kesamaan dan sifat-sifatnya. Himpunan penyelesaian suatu persamaan dapat ditentukan dengan sifat-sifat yang terdapat pada kesamaan, yaitu :

  1. Jika suatu persamaan kedua ruasnya masing-masing ditambah atau dikurangi dengan bilangan yang sama, maka penyelesaiannya tidak berubah.
  2. Jika suatu persamaan kedua ruasnya masing-masing dikalikan dengan bilangan positif yang sama, maka penyelesaiannya tidak berubah.
  3. Jika suatu persamaan kedua ruasnya masing-masing dikalikan atau dibagikan dengan bilangan negatif yang sama, maka penyelesaiannya tidak berubah.

  • Himpunan Penyelesaian Persamaan Linear Dengan Dua Variabel

Himpunan penyelesaian suatu persamaan linear dengan dua variabel dinamakan penyelesaian persamaan tersebut. Mencari penyelesaiannya sama artinya dengan mencari nilai (x,y) yang memenuhi persamaan tersebut sehingga menjadi benar, jika tidak ada ketentuan- ketentuan yang diberikan tentang variabel-variabel itu dianggap pada himpunan bilangan real.

Dalam proses penyelesaian suatu persamaan dengan dua variabel, senantiasa tidak terlepas dari pembahasan kesamaan dan sifat-sifat pada kesamaan yang sudah disebut di atas.

  Kemudian untuk menyelesaikan suatu persamaan kita harus mendapatkan persamaan yang ekwivalen yang paling sederhana. Untuk mengerjakan hal tersebut diusahakan agar variabel-variabel terletak pada suatu ruas ( biasanya ruas kiri), dan konstanta-konstanta pada ruas yang lain, dengan jalan menambah kedua ruas persamaan yang diketahui dengan lawan suku-suku yang bersesuaian.

Posting terkait: