Matematika sering kali dianggap sulit oleh sebagian pelajar, terutama ketika memasuki bab relasi dan fungsi. Padahal, relasi dan fungsi merupakan dasar penting dalam memahami konsep aljabar, grafik, dan kalkulus di tingkat lanjut. Dalam dunia pendidikan, guru sering menyajikan contoh soal relasi dan fungsi untuk membantu siswa memahami hubungan antar himpunan dengan cara yang lebih konkret. Artikel ini akan membahas secara mendetail berbagai contoh soal, penjelasan, serta cara penyelesaiannya agar lebih mudah dipahami.
“Menurut saya, memahami relasi dan fungsi ibarat belajar membaca peta. Jika kita tahu simbol dan arahnya, maka semua jalur perhitungan akan terlihat lebih jelas,” ujar penulis.
Pengertian Relasi dalam Matematika
Relasi dalam matematika berarti hubungan yang mengaitkan anggota satu himpunan dengan anggota himpunan lain. Relasi dapat dinyatakan dalam berbagai bentuk, mulai dari diagram panah, himpunan pasangan berurutan, hingga grafik di bidang koordinat.
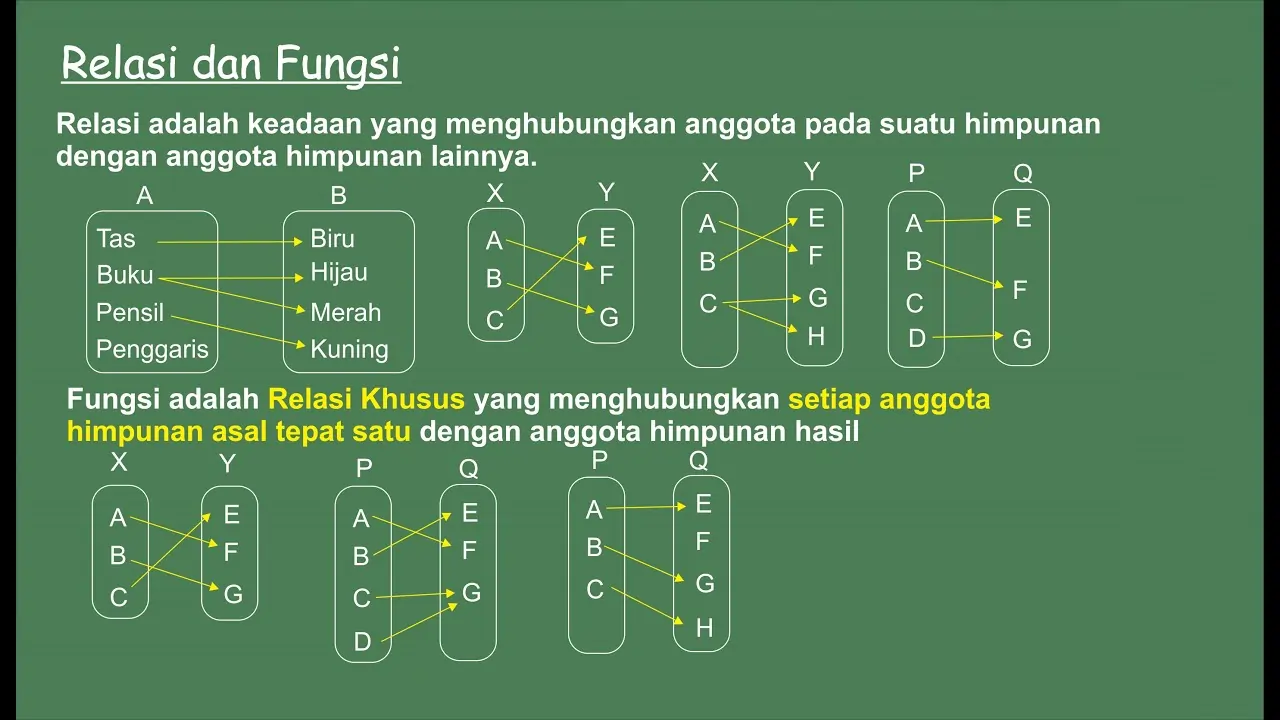
Bentuk Relasi dengan Diagram Panah
Diagram panah sering dipakai karena visualisasinya mudah dipahami. Setiap anggota himpunan A akan dihubungkan dengan anggota himpunan B menggunakan panah.
Relasi dalam Bentuk Pasangan Berurutan
Relasi juga bisa ditulis sebagai kumpulan pasangan berurutan, misalnya {(1,2), (2,3), (3,4)}. Bentuk ini lebih ringkas namun tetap menunjukkan hubungan antar anggota himpunan.
Pengertian Fungsi dalam Matematika
Fungsi merupakan relasi khusus yang menghubungkan setiap anggota himpunan A (domain) dengan tepat satu anggota himpunan B (kodomain). Inilah yang membuat fungsi berbeda dengan relasi biasa. Konsep fungsi sangat penting karena digunakan dalam hampir semua cabang matematika.
Contoh Fungsi dalam Kehidupan Sehari-hari
Misalnya, fungsi yang memetakan setiap siswa ke nomor induknya. Setiap siswa hanya memiliki satu nomor induk, sehingga memenuhi syarat fungsi.
Notasi Fungsi
Jika terdapat fungsi f dari A ke B, ditulis f: A → B. Artinya, setiap anggota A memiliki pasangan tunggal di B.
Contoh Soal Relasi
Berikut beberapa contoh soal yang sering muncul dalam pembelajaran:
Contoh Soal 1
Diketahui himpunan A = {1, 2, 3} dan B = {2, 4, 6}. Tentukan relasi R dari A ke B dengan aturan “x berhubungan dengan y jika y = 2x”.
Penyelesaian
Pasangan berurutannya adalah:
R = {(1,2), (2,4), (3,6)}.
Relasi ini dapat digambarkan dengan diagram panah dari setiap anggota A menuju anggota B yang sesuai.
Contoh Soal 2
Himpunan X = {a, b, c} dan Y = {1, 2}. Tentukan relasi dari X ke Y jika aturan “setiap huruf berhubungan dengan bilangan ganjil”.
Penyelesaian
Karena di himpunan Y hanya ada {1, 2}, maka hanya bilangan 1 yang ganjil. Relasinya adalah {(a,1), (b,1), (c,1)}.
Contoh Soal Fungsi
Fungsi biasanya lebih menantang karena ada syarat khusus yaitu satu anggota domain hanya boleh dipasangkan dengan satu anggota kodomain.
Contoh Soal 1
Diketahui f: A → B dengan A = {1,2,3,4} dan B = {2,4,6,8}. Jika f(x) = 2x, tentukan himpunan pasangan berurutannya.
Penyelesaian
f(1)=2, f(2)=4, f(3)=6, f(4)=8.
Maka f = {(1,2), (2,4), (3,6), (4,8)}.
Contoh Soal 2
Diketahui g: {0,1,2,3} → {0,1,4,9} dengan aturan g(x)=x². Tentukan apakah g merupakan fungsi.
Penyelesaian
g(0)=0, g(1)=1, g(2)=4, g(3)=9.
Setiap anggota domain hanya memiliki satu pasangan di kodomain, sehingga g merupakan fungsi.
Cara Mudah Membedakan Relasi dan Fungsi
Banyak siswa yang masih bingung membedakan relasi dan fungsi. Padahal, ada cara sederhana untuk membedakannya.
Satu Input Satu Output
Jika ada satu anggota domain yang berhubungan dengan lebih dari satu anggota kodomain, maka itu bukan fungsi.
Gunakan Uji Vertikal pada Grafik
Jika grafik suatu relasi dilalui oleh garis vertikal lebih dari satu kali, maka relasi itu bukan fungsi.
“Saya selalu menekankan kepada siswa bahwa fungsi itu harus setia. Satu input hanya untuk satu output. Jika lebih dari satu, berarti bukan fungsi,” ujar penulis.
Latihan Soal Relasi dan Fungsi
Agar lebih memahami, berikut beberapa latihan soal yang bisa dicoba pembaca. Setiap soal disertai pembahasan agar tidak hanya berhenti pada hasil, tetapi juga proses berpikirnya.
Soal 1
A = {2,4,6}, B = {1,2,3,4,5,6}. Tentukan relasi R dari A ke B dengan aturan “x lebih kecil dari y”.
Pembahasan
Untuk x=2 → pasangan { (2,3), (2,4), (2,5), (2,6) }
Untuk x=4 → pasangan { (4,5), (4,6) }
Untuk x=6 → tidak ada karena 6 tidak lebih kecil dari anggota B.
Maka R = {(2,3), (2,4), (2,5), (2,6), (4,5), (4,6)}.
Soal 2
Himpunan X = {1,2,3} dan Y = {a,b,c,d}. Tentukan apakah relasi {(1,a), (2,b), (3,c), (3,d)} merupakan fungsi.
Pembahasan
Anggota 3 dipasangkan dengan dua anggota berbeda yaitu c dan d. Maka ini bukan fungsi, melainkan hanya relasi.
Soal 3
Diketahui fungsi f dengan domain {1,2,3,4,5} dan aturan f(x) = x + 1. Tentukan pasangan berurutannya.
Pembahasan
f(1)=2, f(2)=3, f(3)=4, f(4)=5, f(5)=6.
Maka f = {(1,2), (2,3), (3,4), (4,5), (5,6)}.
Tambahan 10 Soal Latihan Fungsi dengan Pembahasan Singkat
- f(x)=3x, A={1,2,3}
f = {(1,3),(2,6),(3,9)} - f(x)=x², A={-2,-1,0,1,2}
f = {(-2,4),(-1,1),(0,0),(1,1),(2,4)} - Relasi {(1,2),(1,3),(2,4)} apakah fungsi?
Tidak, karena 1 punya dua pasangan. - f(x)=2x+1, A={0,1,2,3}
f={(0,1),(1,3),(2,5),(3,7)} - f(x)=√x, A={0,1,4,9}
f={(0,0),(1,1),(4,2),(9,3)} - Relasi {(a,1),(b,2),(c,3)} apakah fungsi?
Ya, karena setiap domain hanya punya satu pasangan. - f(x)=x-2, A={2,3,4,5}
f={(2,0),(3,1),(4,2),(5,3)} - Relasi {(1,2),(2,2),(3,2)} apakah fungsi?
Ya, karena tiap domain punya satu pasangan, meski kodomain sama. - f(x)=x³, A={-1,0,1,2}
f={(-1,-1),(0,0),(1,1),(2,8)} - Relasi {(1,a),(1,b),(2,c)} apakah fungsi?
Tidak, karena 1 punya lebih dari satu pasangan.
Tabel Ringkas Perbedaan Relasi dan Fungsi
| Aspek | Relasi | Fungsi |
|---|---|---|
| Definisi | Hubungan antara dua himpunan | Relasi khusus yang tiap anggota domain punya satu pasangan |
| Pasangan Input | Bisa lebih dari satu output | Hanya satu output untuk setiap input |
| Representasi | Diagram panah, pasangan berurutan, grafik | Sama, tapi dengan syarat khusus fungsi |
“Menurut saya, semakin banyak latihan soal yang dikerjakan, semakin cepat pula siswa bisa membedakan mana relasi dan mana fungsi. Pembiasaan adalah kunci dalam memahami topik ini,”