Matematika dikenal sebagai ilmu yang penuh dengan logika dan keteraturan. Di antara berbagai konsep penting yang ada, rumus Phitagoras menempati posisi istimewa karena bukan hanya dipelajari di sekolah, tetapi juga banyak diterapkan dalam kehidupan sehari-hari. Rumus ini dianggap sebagai salah satu pondasi utama dalam memahami hubungan antar sisi segitiga siku-siku dan terus menjadi rujukan hingga kini.
Sejarah Rumus Phitagoras
Rumus Phitagoras diambil dari nama seorang filsuf dan matematikawan Yunani kuno bernama Pythagoras, yang hidup pada abad ke-6 SM. Meski demikian, catatan sejarah menunjukkan bahwa prinsip serupa sebenarnya sudah dikenal oleh peradaban Babilonia dan India jauh sebelum masa Pythagoras.
Pythagoras kemudian menjadi tokoh yang mengembangkan serta mempopulerkan teorema ini dalam sistem matematika formal. Ia memimpin sebuah sekolah yang mengajarkan filsafat, musik, dan tentu saja matematika sebagai dasar berpikir logis.
“Sejarah rumus Phitagoras membuktikan bahwa ilmu pengetahuan adalah warisan peradaban, bukan karya individu semata.”
Bunyi Teorema Phitagoras
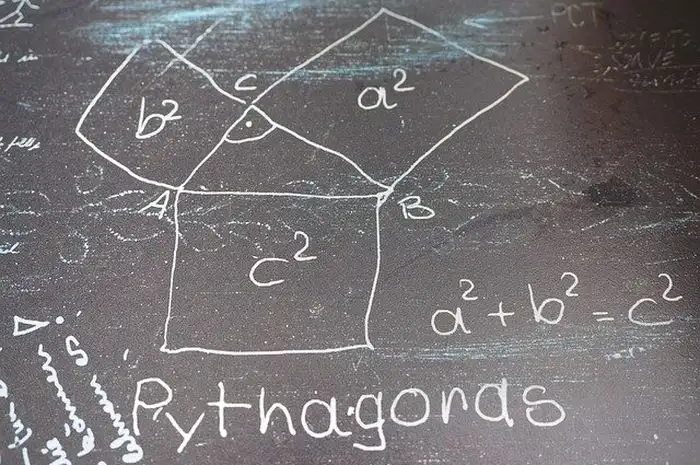
Teorema Phitagoras menyatakan bahwa dalam sebuah segitiga siku-siku, kuadrat panjang sisi miring (hipotenusa) sama dengan jumlah kuadrat dari dua sisi lainnya.
Secara matematis dapat ditulis:
c² = a² + b²
Keterangan:
- c = sisi miring (hipotenusa)
- a = sisi alas
- b = sisi tegak
Rumus sederhana ini menjadi dasar dalam menghitung panjang sisi segitiga, membuktikan sifat-sifat geometri, hingga membantu dalam perhitungan jarak.
Mengapa Rumus Phitagoras Ini Penting?
Rumus Phitagoras bukan hanya sebuah teori abstrak. Ia memiliki penerapan luas di bidang arsitektur, teknik sipil, astronomi, bahkan dalam kehidupan sehari-hari seperti menentukan panjang tangga yang tepat untuk mencapai ketinggian tertentu.
Dalam dunia pendidikan, rumus ini juga sering dijadikan titik awal untuk mengajarkan logika matematika dan pembuktian. Melalui Phitagoras, siswa belajar bahwa matematika adalah ilmu yang bisa diterapkan pada masalah nyata.
Contoh Penerapan dalam Kehidupan Sehari-hari
Salah satu contoh sederhana adalah ketika seseorang ingin mengetahui panjang tangga untuk mencapai dinding setinggi 3 meter dengan jarak alas 4 meter. Dengan menggunakan rumus Phitagoras, panjang tangga dapat dihitung:
c² = 3² + 4²
c² = 9 + 16
c² = 25
c = 5 meter
Dengan demikian, tangga yang dibutuhkan minimal memiliki panjang 5 meter.
“Setiap kali saya melihat tukang bangunan mengukur dengan perhitungan sederhana, saya yakin Phitagoras hadir dalam kehidupan kita tanpa disadari.”
Segitiga Istimewa dalam Phitagoras
Dalam penerapan rumus ini, dikenal pula konsep segitiga istimewa. Beberapa kombinasi sisi segitiga siku-siku memiliki pola tertentu yang sering digunakan, di antaranya:
- Segitiga 3-4-5
- Segitiga 5-12-13
- Segitiga 7-24-25
Segitiga istimewa ini memudahkan perhitungan cepat tanpa harus selalu menghitung dengan akar kuadrat.
Rumus Phitagoras dalam Bidang Arsitektur
Bangunan megah di seluruh dunia, mulai dari piramida Mesir hingga gedung pencakar langit modern, banyak menggunakan prinsip Phitagoras dalam konstruksinya. Dengan menghitung sisi miring dan sudut secara akurat, para arsitek dapat memastikan bangunan berdiri kokoh dan simetris.
Selain itu, perhitungan tangga, atap miring, hingga struktur jembatan juga memanfaatkan teorema ini. Tanpa Phitagoras, perencanaan desain bisa berisiko salah perhitungan.
Phitagoras dalam Teknologi dan Navigasi
Di era modern, rumus ini juga diterapkan dalam teknologi navigasi. Sistem GPS, misalnya, menggunakan prinsip perhitungan jarak antar titik yang melibatkan konsep Phitagoras.
Ilmu komputer pun tidak lepas dari penerapan teorema ini, terutama dalam pemrograman grafis dan pengolahan gambar dua dimensi. Dengan menghitung jarak antar piksel, sistem dapat menghasilkan gambar yang proporsional.
Phitagoras dalam Astronomi
Sejak zaman kuno, astronom memanfaatkan prinsip Phitagoras untuk mengukur jarak antar bintang dan planet. Meskipun kini metode pengukuran lebih canggih, prinsip dasar ini tetap relevan.
Dengan bantuan Phitagoras, manusia bisa memahami hubungan jarak dalam ruang angkasa, yang kemudian berkembang menjadi dasar bagi ilmu trigonometri dan kalkulus.
Pembuktian Teorema Phitagoras
Salah satu aspek menarik dari teorema ini adalah banyaknya cara pembuktian yang bisa dilakukan. Sejarah mencatat ada lebih dari 300 metode berbeda untuk membuktikan kebenaran rumus Phitagoras.
Metode klasik adalah dengan menggambar dua persegi yang sama besar, kemudian membandingkan luasnya dengan susunan segitiga siku-siku di dalamnya. Dari sanalah diperoleh kesimpulan bahwa c² = a² + b².
Rumus Turunan dari Phitagoras
Selain digunakan untuk menghitung sisi segitiga, teorema ini juga melahirkan berbagai rumus turunan. Misalnya, untuk menghitung jarak titik ke titik dalam bidang koordinat dua dimensi:
d = √((x2 – x1)² + (y2 – y1)²)
Rumus ini banyak dipakai dalam geometri analitik, peta digital, hingga aplikasi desain grafis.
Tantangan dalam Pembelajaran Phitagoras
Meski sederhana, tidak sedikit siswa yang merasa kesulitan memahami teorema ini. Salah satu penyebabnya adalah kurangnya pendekatan praktis dalam pembelajaran.
Guru sering kali hanya menekankan hafalan rumus tanpa menunjukkan penerapan nyata. Padahal, jika dikaitkan dengan kehidupan sehari-hari, siswa akan lebih mudah memahami dan mengapresiasi rumus ini.
Phitagoras sebagai Inspirasi Ilmu Pengetahuan
Lebih dari sekadar teorema, Phitagoras adalah simbol dari rasa ingin tahu manusia terhadap keteraturan alam. Ia menunjukkan bahwa dunia bisa dipahami melalui angka dan logika.
Di banyak kesempatan, teorema ini dijadikan pintu masuk untuk menjelaskan betapa luasnya peran matematika dalam kehidupan manusia.
“Bagi saya, Phitagoras adalah bukti bahwa matematika bukan hanya angka di papan tulis, melainkan bahasa universal yang menyatukan peradaban.”
Relevansi Phitagoras di Era Digital
Meski ditemukan ribuan tahun lalu, teorema ini tetap relevan di era digital. Dalam industri gim, desain grafis, animasi, hingga teknologi kecerdasan buatan, Phitagoras hadir sebagai bagian dari algoritma perhitungan yang rumit.
Kehadirannya menunjukkan bahwa pengetahuan klasik dapat bertahan lintas zaman dan terus berkontribusi pada perkembangan teknologi modern.