Persamaan garis lurus merupakan salah satu materi dasar dalam matematika yang sering muncul dalam ujian sekolah maupun tes masuk perguruan tinggi. Konsep ini tidak hanya penting untuk memahami aljabar, tetapi juga menjadi fondasi dalam pembahasan geometri analitik. Banyak siswa yang merasa persamaan garis lurus mudah dipahami jika disertai contoh soal dan pembahasan langkah demi langkah.
Sebagai penulis di portal edukasi, saya percaya bahwa menguasai persamaan garis lurus bukan hanya soal hitungan, tetapi juga soal logika berpikir. “Menurut saya, siswa yang terbiasa melatih soal persamaan garis lurus akan lebih cepat mengasah pola pikir analitisnya. Hal ini terlihat saat mereka mampu menghubungkan konsep garis dengan kehidupan sehari-hari, misalnya menghitung kecepatan atau perbandingan jarak,” ungkap saya dalam sebuah kesempatan.
Pengertian Persamaan Garis Lurus
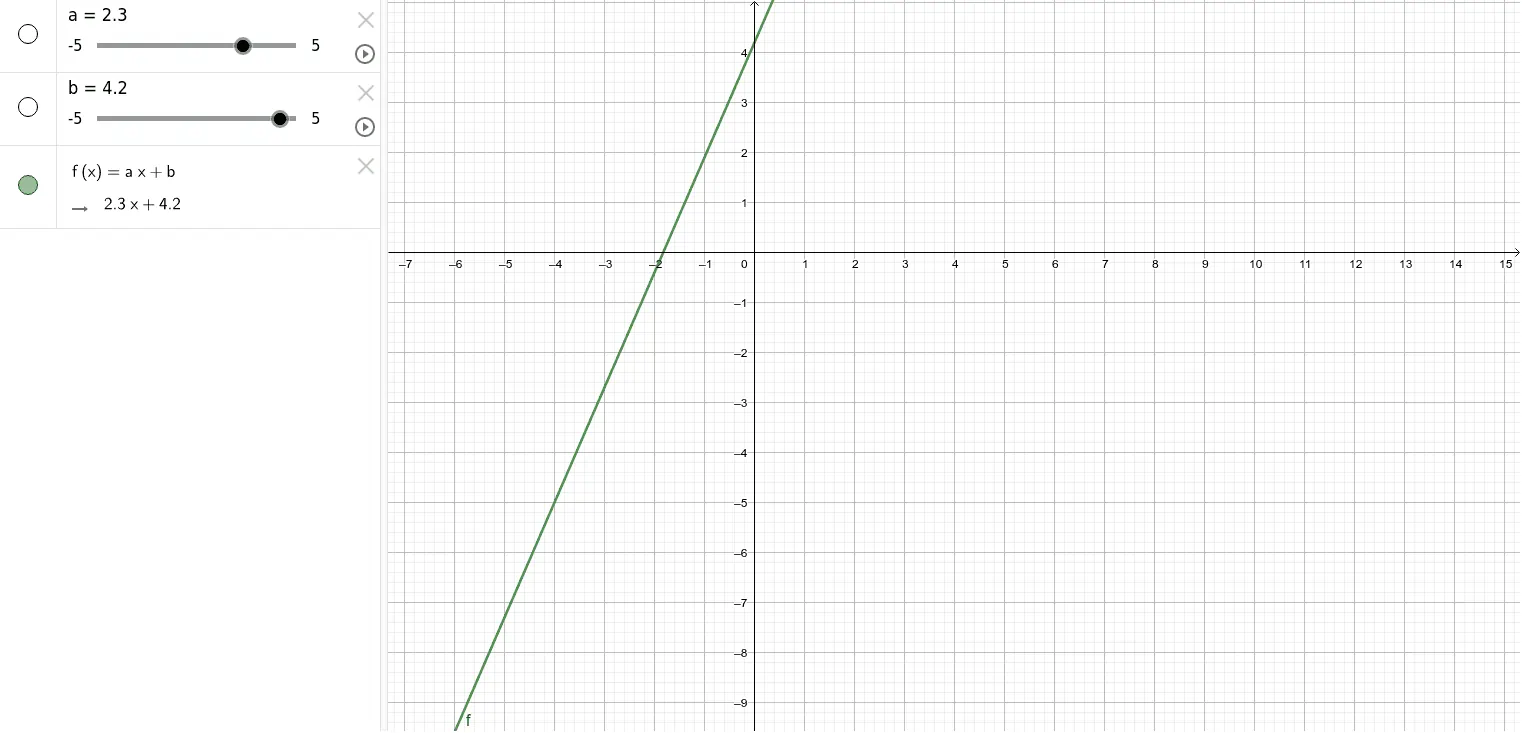
Persamaan garis lurus adalah persamaan aljabar yang menggambarkan sebuah garis pada bidang koordinat kartesius. Secara umum, bentuk persamaan garis lurus ditulis dalam format:
y = mx + c
Keterangan:
- m adalah gradien (kemiringan garis).
- c adalah konstanta yang menunjukkan titik potong dengan sumbu y.
Selain bentuk umum, ada juga bentuk persamaan garis lurus lain seperti bentuk baku dan bentuk titik gradien.
Bentuk-Bentuk Persamaan Garis Lurus
Untuk memahami materi ini, siswa perlu mengenal bentuk-bentuk persamaan garis lurus agar mudah mengidentifikasi saat soal diberikan.
Bentuk Umum
Persamaan garis lurus dalam bentuk umum adalah:
ax + by + c = 0
dengan a, b, dan c merupakan bilangan real, dan a serta b tidak boleh sama-sama nol.
Bentuk Slope Intercept
Bentuk slope intercept atau bentuk kemiringan adalah:
y = mx + c
Bentuk ini paling sering digunakan untuk menggambarkan garis karena lebih mudah dipahami.
Bentuk Titik Gradien
Jika sebuah garis melalui titik (x₁, y₁) dan memiliki gradien m, maka persamaannya adalah:
y – y₁ = m(x – x₁)
Bentuk ini sangat membantu saat soal memberikan titik dan gradien.
Cara Mencari Gradien
Gradien menunjukkan seberapa miring sebuah garis. Cara menghitung gradien berbeda-beda, tergantung informasi yang diberikan.
Gradien dari Dua Titik
Jika garis melewati titik A(x₁, y₁) dan B(x₂, y₂), maka gradien m dihitung dengan:
m = (y₂ – y₁) / (x₂ – x₁)
Gradien Garis yang Tegak Lurus
Jika dua garis tegak lurus, maka hasil kali gradiennya adalah –1.
m₁ × m₂ = –1
Gradien Garis yang Sejajar
Jika dua garis sejajar, maka gradiennya sama.
m₁ = m₂
Contoh Soal Persamaan Garis Lurus
Agar lebih jelas, berikut contoh soal dan pembahasannya secara bertahap.
Contoh Soal 1
Tentukan persamaan garis yang melalui titik (2, 3) dan bergradien 4.
Pembahasan:
Gunakan bentuk titik gradien:
y – y₁ = m(x – x₁)
y – 3 = 4(x – 2)
y – 3 = 4x – 8
y = 4x – 5
Jadi persamaan garisnya adalah y = 4x – 5.
Contoh Soal 2
Tentukan persamaan garis yang melalui titik A(1, 2) dan B(3, 6).
Pembahasan:
Cari gradien terlebih dahulu:
m = (6 – 2) / (3 – 1) = 4 / 2 = 2
Gunakan bentuk titik gradien dengan titik A(1, 2):
y – 2 = 2(x – 1)
y – 2 = 2x – 2
y = 2x
Jadi persamaan garisnya adalah y = 2x.
Contoh Soal 3
Tentukan persamaan garis yang sejajar dengan garis 2x – y + 5 = 0 dan melalui titik (0, –3).
Pembahasan:
Persamaan garis 2x – y + 5 = 0 dapat ditulis ulang menjadi:
y = 2x + 5
Sehingga gradiennya adalah 2.
Garis sejajar memiliki gradien yang sama, maka gunakan titik (0, –3):
y – (–3) = 2(x – 0)
y + 3 = 2x
y = 2x – 3
Jadi persamaan garisnya adalah y = 2x – 3.
Contoh Soal 4
Tentukan persamaan garis yang tegak lurus dengan garis y = –½x + 4 dan melalui titik (2, 1).
Pembahasan:
Gradien garis y = –½x + 4 adalah –½.
Jika tegak lurus, gradien barunya adalah kebalikan negatif: m = 2.
Gunakan bentuk titik gradien:
y – 1 = 2(x – 2)
y – 1 = 2x – 4
y = 2x – 3
Jadi persamaan garisnya adalah y = 2x – 3.
Aplikasi Persamaan Garis Lurus dalam Kehidupan Sehari-hari
Persamaan garis lurus tidak hanya ada di buku pelajaran. Dalam kehidupan nyata, konsep ini bisa ditemui pada banyak hal. Misalnya, menghitung biaya transportasi ojek online dengan tarif dasar ditambah biaya per kilometer bisa dimodelkan dengan persamaan garis lurus.
Contoh Kasus
Sebuah ojek online memiliki tarif awal Rp10.000 ditambah Rp2.000 untuk setiap kilometer. Jika jaraknya x km, maka total biaya adalah:
y = 2000x + 10000
Dengan model ini, siswa bisa langsung melihat hubungan nyata antara matematika dan kehidupan.
“Menurut saya, siswa akan lebih semangat belajar matematika jika bisa melihat aplikasinya dalam kehidupan sehari-hari. Persamaan garis lurus adalah salah satu topik yang paling mudah dihubungkan dengan situasi nyata, mulai dari tarif transportasi hingga grafik pertumbuhan ekonomi,” tulis saya sebagai refleksi pribadi.