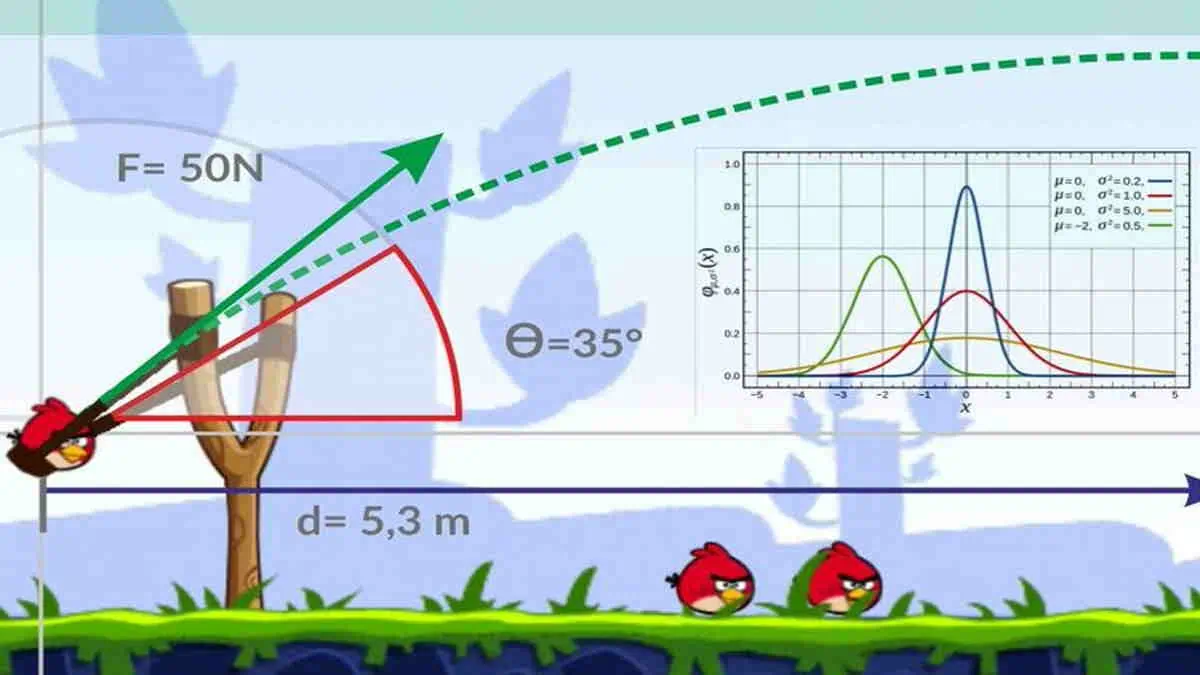
Gerak parabola adalah salah satu materi fisika yang sering muncul dalam soal-soal ujian sekolah maupun tes masuk perguruan tinggi. Memahami gerak parabola sangat penting, karena konsep ini tidak hanya melatih logika berpikir siswa, tetapi juga memperkuat pemahaman dasar-dasar fisika dalam kehidupan sehari-hari. Artikel ini akan membahas berbagai contoh soal gerak parabola lengkap dengan pembahasan, sehingga diharapkan pembaca dapat lebih mudah mempelajari dan memahami materi ini.
Pengertian Gerak Parabola
Sebelum masuk ke contoh soal, penting untuk memahami terlebih dahulu apa itu gerak parabola. Gerak parabola merupakan perpaduan antara gerak lurus beraturan (GLB) pada sumbu horizontal (sumbu x) dan gerak lurus berubah beraturan (GLBB) pada sumbu vertikal (sumbu y). Kombinasi kedua gerak ini menyebabkan lintasan benda membentuk lengkungan seperti parabola.
Gerak ini sering dijumpai pada berbagai aktivitas sehari-hari, seperti bola yang dilempar ke udara, peluru yang ditembakkan dari meriam, atau air yang disemprotkan dari selang.
Rumus Dasar Gerak Parabola
Sebelum membahas contoh soal, berikut adalah beberapa rumus dasar yang sering digunakan dalam penyelesaian soal gerak parabola:
- Komponen kecepatan awal:
- Vx = Vo cos θ
- Vy = Vo sin θ
- Jarak horizontal maksimum (Xmax):
- Xmax = (Vo² sin 2θ) / g
- Waktu di udara (t):
- t = (2 Vo sin θ) / g
- Ketinggian maksimum (Hmax):
- Hmax = (Vo² sin² θ) / (2g)
Keterangan:
- Vo = kecepatan awal (m/s)
- θ = sudut elevasi (derajat)
- g = percepatan gravitasi (9,8 m/s²)
- Vx = komponen kecepatan pada sumbu x
- Vy = komponen kecepatan pada sumbu y
Contoh Soal Gerak Parabola dan Pembahasannya
Contoh Soal 1: Menentukan Jarak Maksimum
Seorang pemain basket melempar bola dengan kecepatan awal 20 m/s membentuk sudut 30° terhadap horizontal. Berapakah jarak terjauh yang dapat dicapai bola tersebut? (g = 10 m/s²)
Penyelesaian:
- Diketahui:
- Vo = 20 m/s
- θ = 30°
- g = 10 m/s²
- Mencari jarak maksimum (Xmax): Xmax = (Vo² sin 2θ) / g
Xmax = (20² × sin 60°) / 10
Xmax = (400 × 0,866) / 10
Xmax = 346,4 / 10
Xmax = 34,64 m
Jadi, jarak maksimum bola adalah 34,64 meter.
Contoh Soal 2: Menentukan Ketinggian Maksimum
Sebuah bola dilempar dengan kecepatan awal 15 m/s pada sudut 45° terhadap bidang datar. Hitunglah ketinggian maksimum yang dapat dicapai bola tersebut! (g = 10 m/s²)
Penyelesaian:
- Diketahui:
- Vo = 15 m/s
- θ = 45°
- g = 10 m/s²
- Mencari ketinggian maksimum (Hmax): Hmax = (Vo² sin² θ) / (2g)
Hmax = (15² × (sin 45°)²) / (2 × 10)
Hmax = (225 × (0,707)²) / 20
Hmax = (225 × 0,5) / 20
Hmax = 112,5 / 20
Hmax = 5,625 m
Jadi, ketinggian maksimum bola adalah 5,625 meter.
Contoh Soal 3: Menentukan Waktu yang Diperlukan Benda di Udara
Sebuah peluru ditembakkan dengan kecepatan awal 50 m/s dan sudut elevasi 37°. Hitunglah berapa lama peluru tersebut berada di udara sebelum jatuh ke tanah! (g = 10 m/s²)
Penyelesaian:
- Diketahui:
- Vo = 50 m/s
- θ = 37°
- g = 10 m/s²
- Mencari waktu di udara (t): t = (2 Vo sin θ) / g
t = (2 × 50 × sin 37°) / 10
t = (100 × 0,6018) / 10
t = 60,18 / 10
t = 6,018 s
Jadi, waktu yang diperlukan peluru di udara adalah sekitar 6,018 detik.
Contoh Soal 4: Menentukan Titik Tertinggi dari Lintasan
Sebuah bola dilempar dari tanah dengan kecepatan awal 18 m/s pada sudut 60°. Tentukan posisi titik tertinggi lintasan bola!
Penyelesaian:
- Diketahui:
- Vo = 18 m/s
- θ = 60°
- g = 10 m/s²
- Komponen kecepatan awal vertikal: Vy = Vo sin θ = 18 × sin 60° = 18 × 0,866 = 15,588 m/s
- Ketinggian maksimum (Hmax): Hmax = (Vy²) / (2g)
Hmax = (15,588²) / (2 × 10)
Hmax = (243,13) / 20
Hmax = 12,16 m
Jadi, titik tertinggi lintasan bola adalah 12,16 meter di atas tanah.
Contoh Soal 5: Menentukan Posisi Benda Setelah Waktu Tertentu
Sebuah batu dilempar dengan kecepatan awal 25 m/s membentuk sudut 53° terhadap horizontal. Tentukan posisi batu (jarak horizontal dan ketinggian dari tanah) setelah 2 detik! (g = 10 m/s²)
Penyelesaian:
- Diketahui:
- Vo = 25 m/s
- θ = 53°
- g = 10 m/s²
- t = 2 s
- Komponen kecepatan awal:
- Vx = Vo cos θ = 25 × cos 53° = 25 × 0,6018 = 15,045 m/s
- Vy = Vo sin θ = 25 × sin 53° = 25 × 0,7986 = 19,965 m/s
- Jarak horizontal setelah 2 detik: x = Vx × t = 15,045 × 2 = 30,09 m
- Ketinggian dari tanah: y = Vy × t – 0,5 × g × t²
y = 19,965 × 2 – 0,5 × 10 × (2²)
y = 39,93 – 20
y = 19,93 m
Jadi, setelah 2 detik, posisi batu berada pada jarak horizontal 30,09 meter dan ketinggian 19,93 meter dari tanah.
Tips dan Trik Menyelesaikan Soal Gerak Parabola
Untuk memudahkan dalam mengerjakan soal-soal gerak parabola, pahami dan hafalkan rumus-rumus dasar yang telah dijelaskan di atas. Selain itu, biasakan membuat sketsa peristiwa dan menguraikan komponen kecepatan awal menjadi sumbu x dan y.
“Menurut saya, menguasai soal-soal gerak parabola itu ibarat memahami kehidupan: kadang harus fokus ke dua arah berbeda dalam satu waktu, agar sampai ke tujuan dengan tepat.” — Redaksi Passinggrade.co.id
Aplikasi nyata dalam kehidupan sehari-hari
Gerak parabola bukan sekadar teori, namun juga aplikasi nyata dalam kehidupan sehari-hari. Melalui latihan mengerjakan berbagai contoh soal, siswa dapat memahami konsep ini secara menyeluruh dan siap menghadapi berbagai ujian. Kunci utamanya adalah memahami konsep, menguasai rumus, dan rajin berlatih. Semoga artikel ini membantu Anda untuk semakin memahami gerak parabola dan siap menghadapi soal-soal fisika di sekolah maupun ujian seleksi masuk perguruan tinggi.