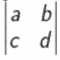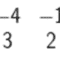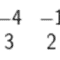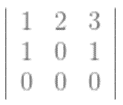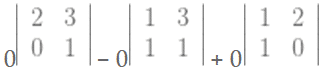Pengertian Determinan Matriks
Daftar Isi Artikel
Determinan Matriks ialah suatu bilangan real yang diperoleh dari suatu proses dengan aturan tertentu terhadap matriks bujur sangkar.
Determinan dinyatakan sebagai jumlah semua hasil kali dasar bertanda dari matriks bujur sangkar A. Determinan dari sebuah matriks bujur sangkar A’ dinotasikan dengan det(A), atau |A|.
Jenis-jenis Determinan Matriks
a. Determinan Matriks Ordo 2 × 2
Misalkan A = 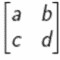
Dengan demikian, dapat diperoleh rumus det A sebagai berikut.
Contoh Soal 1 :
Tentukan determinan matriks-matriks berikut:
Penyelesaian :
b. Determinan Matriks Ordo 3 × 3 (Pengayaan)
Jika A = 
determinan A dinyatakan dengan det A =
Ada 2 cara yang dapat digunakan untuk menentukan determinan matriks berordo 3 × 3, yaitu aturan Sarrus dan metode minor-kofaktor.
- Aturan Sarrus
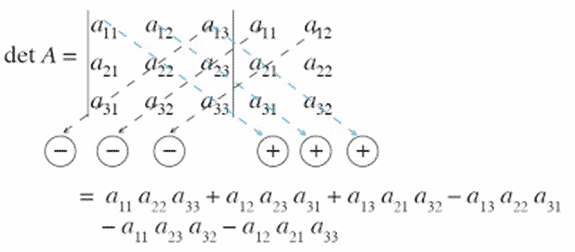
Untuk menentukan determinan dengan aturan Sarrus, perhatikan alur berikut. Misalnya, kita akan menghitung determinan matriks A3 × 3. Gambaran perhitungannya adalah sebagai berikut.
- Metode Minor-Kofaktor
Misalkan matriks A dituliskan dengan [aij]. Minor elemen aij yang dinotasikan dengan Mij adalah determinan setelah elemen-elemen baris ke-i dan kolom ke-j dihilangkan. Misalnya, dari matriks A3 × 3 kita hilangkan baris ke-2 kolom ke-1 sehingga :
Akan diperoleh M21 = 
Kofaktor elemen aij, dinotasikan Kij adalah hasil kali (–1)i+j dengan minor elemen tersebut. Dengan demikian, kofaktor suatu matriks dirumuskan dengan :
Kij = (–1)i+j Mij
Dari matriks A di atas, kita peroleh misalnya kofaktor a21 dan a13 berturut-turut adalah
Kofaktor dari matriks A3 × 3 adalah kof(A) =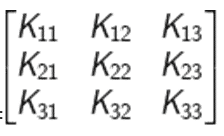
Nilai dari suatu determinan merupakan hasil penjumlahan dari perkalian elemen-elemen suatu baris (atau kolom) dengan kofaktornya. Untuk menghitung determinan, kita dapat memilih dahulu sebuah baris (atau kolom) kemudian kita gunakan aturan di atas.
Sifat-Sifat Determinan Matriks
Berikut sifat-sifat determinan yang terdapat pada matriks.
- Jika A adalah sebarang matriks kuadrat yang mengandung sebaris bilangan nol, maka det(A) = 0.
Contoh :
dengan menggunakan Aturan Kofaktor, maka
= a31M31 – a32M32 + a33M33
= 0(2.1 – 3.0) – 0(1.1 – 1.3) + 0(1.0 – 1.2)
= 0
2. Jika A adalah matriks segitiga n x n, maka det(A) adalah hasil kali entri-entri pada diagonal utama, yakni det(A) = a11a22… ann
Contoh :
= a31M31 – a32M32 + a33M33
= 0(1.1 – 3.3) – 0(2.1 – 0.3) + 3(2.3 – 0.1)
= 0 – 0 + 3.2.3
= 18
Hasil ini sama dengan perkalian entri pada diagonal utama yaitu 2 x 3 x 3 = 18
3. Misalkan A’ adalah matriks yang dihasilkan bila baris tunggal A dikalikan oleh konstanta k, maka det(A’) = k det(A)
Contoh :
berdasarkan Sifat 3 maka det(kA) = det(A’) = 4.3.3 = 36
karena det(A) = 18 dan k = 2 maka k.det(A) = 2.18 = 36
jadi, det(A’) = k.det(A)
4. Misalkan A, A’ dan A” adalah matriks n x n yang hanya berbeda dalam baris tunggal, katakanlah baris ke-r, dan anggap bahwa baris ke r dari A” dapat diperoleh dengan menambahkan entri-entri yang bersesuaian dalam baris ke-r dari A dan dalam baris ke-r dari A’, maka det(A”) = det(A) + det(A’) [hasil yang serupa juga berlaku untuk kolom]
Contoh :
misal
A = 
A’ = 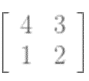
dan A” = A + A’ = 
jadi det(A”) = det(A) + det(A’) = -5 + 5 = 0
Kesimpulan
Pada dasarnya dalam kehidupan sehari-hari kita sering berhadapan dengan persoalan yang apabila kita telusuri ternyata merupakan masalah matematika. Dengan kata lain kita selalu bersentuhan dengan persoalan-persoalan yang berkaitan dengan matematika entah itu kita sadari ataupun tidak. Agar mudah difahami maka persoalan tersebut diubah kedalam bahasa atau persamaan matematika supaya persoalan tersebut lebih mudah diselesaikan. Tetapi terkadang suatu persoalan sering kali memuat lebih dari dua persamaan dan beberapa variabel, sehingga kita mengalami kesulitan untuk mencari hubungan antara variabel-variabelnya.
Adapun matriks sendiri merupakan susunan elemen-elemen yang berbentuk persegi panjang yang di atur dalam baris dan kolom dan di batasi sebuah tanda kurung di sebut matriks.